The Mandelbrot and Julia sets are based on a simple iteration:

X(n+1) = X(n) * X(n) + c

I’m going to keep this explanation simple. Use the powers of your favorite web search engine, or watch a video, to dive into the gritty details. There is a Wikipedia page which has many details, for the more advanced.

The values in the iteration above are complex numbers, normally expressed as a + bi, and the math with complex numbers is slightly different than with real numbers. There is an excellent series of videos explaining complex numbers in the video area. Really. Even if you already know what complex numbers are, watch that video series. Its highly entertaining.

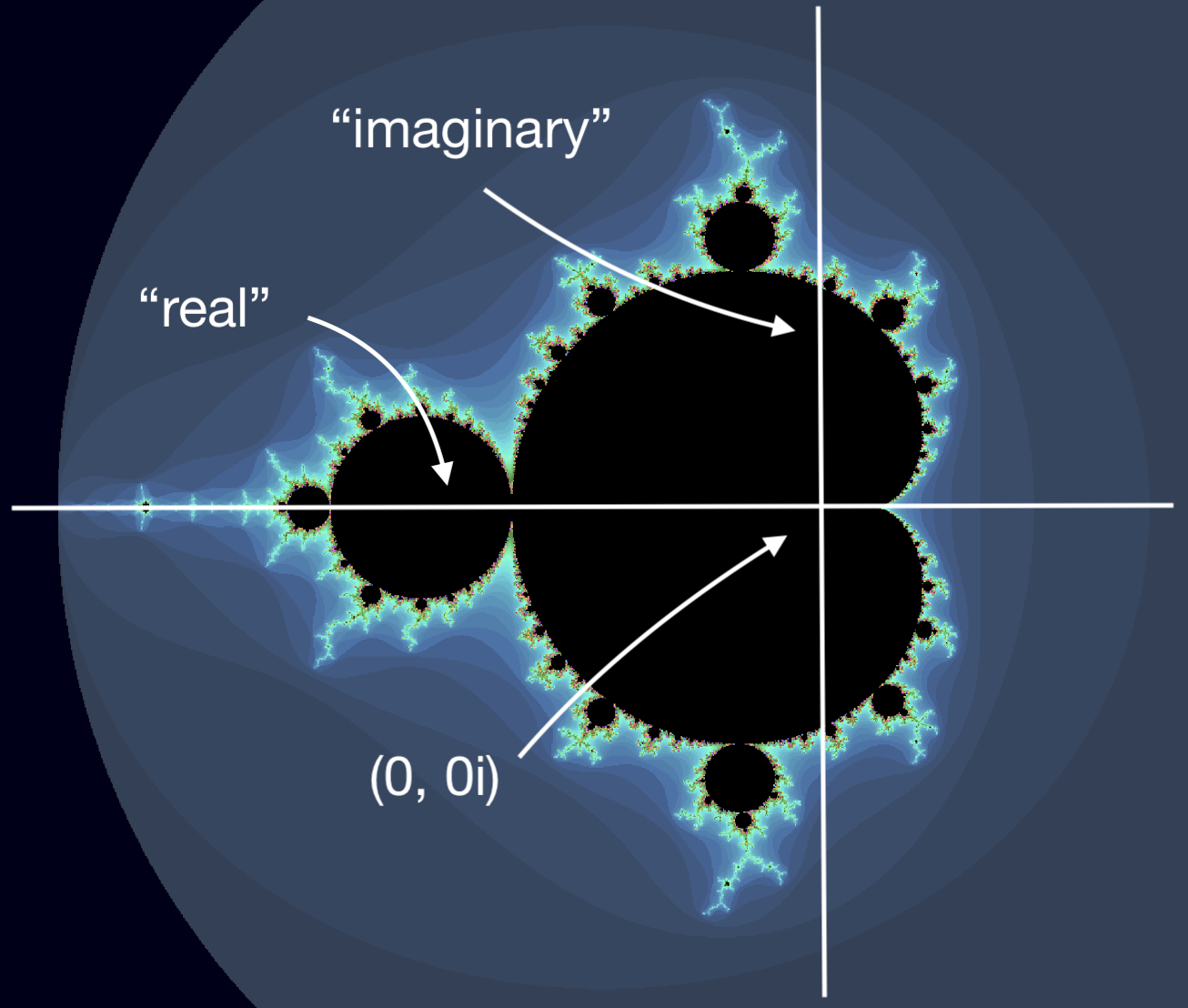
When you see a picture of a Mandelbrot set, you are looking at a graph of the complex number plane, where real numbers, the “a” component, run left and right, and the imaginary component runs up and down.

Its a set!

Consider the word set in the phrase Mandelbrot set. Sets have the propery were things are either in a set or not in a set. There is an inside/outside, member/not-member property to all sets. What the Mandelbrot iteration is doing is classifying points as being either inside or outside the set.

Complex points that are inside the Mandelbrot set are typically drawn as black pixels. Points that are outside the set are assigned a color, and this is where things start to become more interesting.

The iteration.

The equation for the Mandelbrot set is given at the top of this page. Its a simple iteration.

X(0) = 0 + c
X(1) = X(0) * X(0) + c
X(2) = X(1) * X(1) + c
X(3) = X(2) * X(2) + c
...

The iteration continues until we determine whether or not the initial point was inside or outside the set. The point is outside the set if, as the iteration continues, the point explodes off to infinity. Inside points are all of the points which do not expode and get larger and larger. Inside points remain relatively local. Inside points remain bounded where outside points are unbounded.

The path the initial point takes as it jumps around the complex number plane is called its orbit. You can view Mandelbrot and Julia set orbits in Fractally. Some of the orbits are beautiful. If you choose a point with a low iteration count, you should be able to visually examine where the initial point iterated to, for each of its steps until it escapes.

Its beyond the scope of this discussion, but its been shown that as soon as a point moves beyond 2 units away from the origin of the complex number plane, that it will escape and only get larger and larger. Points less than 2 may explode or continue to remain bounded, you need to keep iterating to find out. Once a point is larger than 2, we know its outside.

(If you want to develop some intuition on this property, run the app and show the iterations editor. Then decrease the number of iterations to 2. The largest circle shown has a radius of 2.1 units, slightly larger than 2 so that you can examine what happens at that radius. Slowly increase the number of iterations and examine what is going on.)

If a point is inside the set, then the iteration can continue forever. We stop iterating at some arbitrary maximum value. If a point hasn’t escaped before it hits the maximum number of iterations, then its considered in the set.

Note that we can answer the question: is a point outside the set? in a definitive way. If a point escapes, its outside. However, the opposite question, is a point inside the set? can only be approximated. We iterate to a maximum number of iterations and use that as the approximation. But, in general, we don’t know if we were to continue iterating one more time if the point would escape or not. If we stop after 400 iterations, and a point hasn’t escaped, would iterating 800 times allow it to escape? The outside test is exact. The inside test is an approximation.

Assigning a color.

Given an initial point that we want to test for being inside or outside the set, we iterate the equation to find out. Once the point becomes larger than two, we can stop the iteration. as we know it escapes and is outside the set.

The number of iterations it takes to discover whether or not a point escapes or not is used to assign a color to the pixel. If a point takes 1 iteration to escape, its assigned color one. If a point takes two iterations to escape, its assigned color two.

As the maximum number of iterations is known, we need a color table with colors for each possible iteration count, from 0 to the maximum. There are a number of color tables provided in the app. You can create your own color table if you don’t mind doing a little coding. See fractally files for some more detail.

That’s all.

That’s really all there is to it. Every pixel on the screen is assigned a complex number, in a grid, using the scroll and zoom values to define the visible portion of the complex number plane. The iteration is performed for each complex number in the grid, and we determine if the point is inside or outside, recording the number of iterations it took to decide. This iteration count is used to assign a color to the pixel.

Julia sets.

The initial iteration in the Mandelbrot set is this equation, where c is the complex number assigned to the pixel based on its location in the screen grid:

X(0) = 0 + c

The Julia set is only slightly different:

X(0) = c * c + seed

Again, c is the pixel value, and seed is an arbitrary value. As Fractally can show both the Mandelbrot and Julia sets at the same time, the value of seed is the complex number at the center of the Mandelbrot image. As you zoom and scroll the Mandelbrot view, the seed changes and the Julia set image will update.

Mandelbrot and Julia set orbits.

Given a point that we want to determine is inside or outside the Mandelbrot set, we iterate to see if the point escapes or not, stopping after some arbitrary maximum number of iterations.

The orbit is the path of the initial point as it moves through the iteration. The app draws the first point in white, and all following points are assigned colors that progress from red through yellow, green, cyan to blue. All points are connected with a thin line.

The orbits can take on iteresting shapes.

Its connected! And other cool properties.

As a teaser, do you know how the Fibonacci numbers appear in the Mandelbrot set? How about where the value of Pi shows up? There are videos on these topics in the Videos page.

The Wikipedia page also discusses some of the fascinating properties of the Mandelbrot set.

One interesting property is that the Mandelbrot set is connected. This property says that all of the inside areas of the Mandelbrot set are somehow connected to the other inside areas. If you zoom into some inside area far outside the main bulb, try zooming in and trying to find the filament that connects that area to the other inside areas.

When viewing Julia sets, if the point in the mandelbrot set is inside (black) then all of the inside points in the Julia set will be connected. If the point in the Mandelbrot set is outside, then there may be inside regions in the Julia set, but they are not connected to the others.

Note that the center of the Julia set is the same as the point in the Mandelbrot set it is associated with. The center of the Julia set will have the same color and same general characteristics as the region surrounding the seed point in the Mandelbrot set.